作者:郭晓娜
学习中遇到的分类任务中的评价指标有准确率(Accuracy)、FPR、FNR、Recall、Precision、F-score、MAP、ROC曲线和AUC等,回归任务中的指标有(r)MSE、MAE、CC/PCC等。有这么多种评价指标,于是希望能按自己的理解梳理这些评价指标存在的意义、计算方法和应用场景。
正文:
机器学习中有很多评价指标,实际上,不同的评价指标就是用不同的方法来评价系统的好坏,或者如果有两个系统,来比较两个系统哪个更好一点。
通常,评价指标是一个具体的数字,代表系统在某项任务上的准确程度或者不准确的程度。对于一个分类任务而言,准确率(accuracy)是最基本的评价指标,即分类正确所占的百分比。然而这些基本的评价指标往往不能很好的反映系统的性能,可能会导致做出较差的判断,选择合适的评价指标有助于选出更适合于当前任务的算法。
评价指标是建立在不同的机器学习任务上的,主要分为三大类:
(1) 对于分类任务而言,评价指标关注的是系统分类正确的能力,会去计算对所有需要分类的样本,有多少分对了,多少分错了;
(2) 对于回归任务而言,不像分类任务一样去预测样本的类别,而是预测具体的数字,例如系统预测值为0.2999,而真实值是3,这样的话,可能预测出来的值永远都是错的,不能再去计算有多少是预测正确多少是预测错误了,这时候要关注的是预测值和真实值之间的差别,而不是正确或者错误;
(3) 最后,对于没有标记信息的无监督学习任务的评价指标关注的是系统对数据的描述的好坏,这类任务的评价非常难。
分类任务:
首先介绍几个基本概念,在此基础上再去组合计算一些指标。
TP、FP、TN、FN 概念:
考虑一个二分类的问题,系统需要将样本分为真(positive),假(negative)两类。
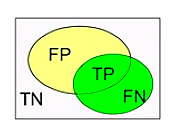
下图的方框代表所有需要预测的样本,黄色圆圈内代表系统预测是真(positive)的样本,绿色圆圈内代表实际情况为真(positive)的样本。
所以黄绿交叉的部分是系统预测为真,实际情况也是真,系统预测正确(True)的True Positive,TP;
黄色圆圈以外的绿色部分是系统预测为假而实际上为真的样本,系统预测错误(False)的False Negatives,FN;
绿色圆圈以外的黄色部分即为系统预测为真,然而实际为假的样本,系统预测错误(False)的False Positives,FP;
最后,灰色部分为系统预测为假,实际也为假,系统预测正确(True)的True Negatives,TN。

上图右边的图可以表示为左边的表格,这个表格被称为混淆矩阵(Confused Matrix)。
对二分类问题而言,混淆矩阵有两行两列,行代表实际情况,第一行表示实际为真,第二行表示实际为假;列代表系统预测情况,第一列表示系统预测为真,第二列表示预测为假。这样的混淆矩阵就把样本分为了上述四类。
可以看出,系统分类正确的TP和TN在混淆矩阵的对角线上,而分类错误的样本在非对角线上。所以我们希望混淆矩阵对角线上的值更大,而非对角线上的值更小。
如果是多分类问题,比如10类,那么混淆矩阵将会是十行十列的矩阵,但是与二分类相同的是,对角线上的部分是系统分类正确的部分,所以依旧希望对角线上的值更大,而对角线以外的部分都是分类错误的部分。
现在基于上面介绍的概念TP、FP、TN、FN来构建不同的指标:
Accuracy
最简单的是错误率和正确率(准确率),错误率即分类错误的样本数量与总样本数量的比例,用上面的概念来表示,分类错误的样本有两类:实际为假的错分为真的FP和实际为真的错分为假的FN,再除以总样本数,即四个值相加。准确率为1减去错误率。

这两个是评价分类系统好坏的基本指标,但是对于分布不均衡的样本,即对于样本中正例(Positive)数量远远少于反例(Negative)的情况,这两个指标将不再可靠。
比如说系统的任务是预测接下来的24小时会不会发生地震,或者是预测某网页和用户输入的关键词是否相关,而大部分时候都不会发生地震,海量网页中绝大多数的网页都和用户的请求不相关,此时只要系统永远预测不会发生地震或者不相关,系统就会得到一个相当高的准确率。因此准确率在系统预测小概率事件时会很具有误导性。
在预测小概率事件的分类问题中,准确率的问题就在于,使用准确率作为评价指标很可能会误导我们去选择错误的分类器。这里多举一个例子:
假设我们要预测某篇文章的作者是否会得诺贝尔奖,我们收集了一些文章,只有极少的文章作者是诺贝尔奖得主,用红色加号表示。有两个系统A和B,系统A正确的分出了两个诺贝尔得主的文章,但是也错分了几个,系统B是只会预测否(Negative),无论什么文章都预测其作者不是诺贝尔奖得主。

如果让人去选择,应该会更倾向于系统A,至少会给出一些正例的信息,但如果用准确率作为评价指标,将会更倾向于选择错误率更少的系统B,系统A分错了四个样本,而系统B只分错了两个。可见,准确率更高的系统不一定是更好的系统。
FPR、FNR、Recall、Precision
为了构建更好的评价指标,要利用上面的四个概念,进行一些组合:

名字很长,但含义好理解:
False Alarm rate,又称False Positive rate,是所有实际为假的样本中有百分之多少被系统错分为真了。
Miss rate,又称False Negative rate,是所有实际为真的样本中有百分之多少被系统错分为假了。
Recall,又称True Positive rate,是所有实际为真的样本中有百分之多少被系统正确分为真了。这个值又称召回率,是和Miss rate加起来为1。
Precision,是所有系统预测为真的样本中有百分之多少实际上也是真的。
最后这两个值很有用,但经常容易弄混,它们两个是关注不同的信息的,Recall关注的是真正的正例中我们错过了多少,如果所有的正例我们都判断出来了,Recall值就为1;Precision关注的是我们所预测为真的那些样本有多少实际不是真,系统给了我们多少‘垃圾’,如果系统预测出的正例全都真的是正例,那么Precision的值为1。注意它们俩的区别,一个是TP占实际为真的样本的比例,一个是TP占系统预测为真的样本的比例。
以上的四个值,很有意思,但是它们其中任何一个单独都不足以成为好的指标,用最笨的分类器就可以使上面的单个指标达到100%或者0%.比如说将所有样本都预测为真的系统可以得到100%的Recall,将所有样本都预测为假的系统可以得到0%的False Alarm rate。
这些指标一般都是成对出现的,比较常见的是Recall和Precision,用于很多领域,Miss rate和False Alarm rate经常用于文献检测任务,True Positive rate和False Positive rate经常用于文献分类任务等。
但是有时,我们需要单独的一个数字来表示系统性能,比如说,当我们想通过脚本自动的从众多分类器中选择最佳的那一个时,我们需要一个数字;比赛中,大家都在做同样的任务,我们需要一个数字去比较哪个最好,哪个第二……
如何利用上面的值去组合出一个合理的评价指标呢,这是根据不同的领域而定的。
Cost
还举预测地震的例子,把系统预测错误的两种情况的代价量化出来:
False Positive:预测地震而实际没有的话,这个代价可能是为了预防地震而采取的行动,人员疏散以及随之带来的经济损失;
False Negative:地震了而没有预测出来,这个代价就不仅仅是经济上的了,还可能会有人员伤亡等。
对于这种事件检测系统,经常会使用FPR、FNR的加权平均Cost:

F-score
其他的领域使用不同的标准,例如信息检索中常用到F-score,是Recall和Precision的调和平均(harmonic mean),是它俩的组合:
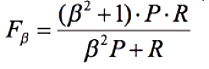
F-score有一个参数β,通过调节这个参数给Recall和Precision不同的权值,这个参数为1时为F1,此时Recall和Precision的权重相同。
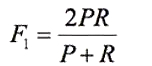
可以看到,当Recall或者Precision的值很小的时候,F值也将很小,因此不管其中一个值多高,只要另一个值很小,F就会很小。
F和Accuracy有什么不同?
F的计算中没有使用到True Negatives,而在不均衡样本预测中,这恰恰是大量的你不关注的信息,这也是导致Accuracy不可靠的因素。
ROC曲线、AUC
许多分类器会为每个样本产生一个实值分数或概率预测,将这个预测的值和一个分类阈值(threshold)相比,大于阈值则预测为真,小于阈值则预测为假。实际上,可以将测试样本按照得分高低进行排序,得分最高的,最可能为正例的排在前面,得分低的排在后面,这时,分类任务相当于在这个排序中以某个“截断点”(cut point)将样本分成两部分,前一部分判成正例,后一部分则判成反例。
我们可以发现,选择不同的阈值,即选择不同位置作为截断点可以得到不同的FPR、FNR、Recall、Precision,这些性能指标是阈值的函数,随着阈值的变化而变化。如果我们想评价这个排序本身的好坏,ROC曲线会是一个有力的工具。
ROC曲线不会指定一个固定的阈值,而是会尝试所有可能的阈值(截断点),在每一种可能的阈值下,计算出多对TPR和FPR,并画出曲线:

举个例子:
预测邮件是否为垃圾邮件(spam),绿色代表是垃圾邮件,假设截断点右侧预测为垃圾邮件,左侧为非垃圾邮件。

当阈值设定使得截断点在t1时,TPR将会是4/8,即8个垃圾邮件里正确分出了4个,FPR为3/15,即15个非垃圾邮件里3个错分成了垃圾邮件。截断点在t2时,TPR将达到1,FPR将会是15个非垃圾邮件了错分了9个为垃圾邮件。
将阈值从最小到最大进行遍历(即例子中的从最右到最左),TPR和FPR都将会从最小逐渐增大到1。
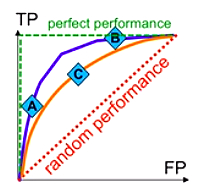
绿色的虚线拥有最佳的性能,在(0,1)点处达到最佳性能,红色的虚线是随机预测的系统的曲线。
取不同的阈值可以得到ROC曲线上的不同的点,假如有A、B是蓝色系统上的点,C是橘色系统上的点,每个点都有一对儿值,直接去比较这三个点是比较难的。
如果通过ROC曲线发现,蓝色系统的曲线可以将橘色系统的曲线完全包住,则可以断言:前者的性能优于后者。因为不管怎么去选取阈值,蓝色系统都可以得到比橘色更好的性能。对于任意给定的FPR,蓝色曲线都可以得到更高的TPR,对于任意给定的TPR,蓝色曲线都可以得到更低的FPR。
如果两个系统的曲线交叉,则可以比较ROC曲线下的面积,即AUC(Area Under ROC Curve),理想为1,随机预测为1/2,越大越好。
MAP
Mean Average Precision也是很常用的指标,用于可以给出候选预测结果排序(或者分数)的系统。
MAP是多用于信息检索领域的,先看一下信息检索领域的MAP计算例子,再类比到多分类任务中。
先举一个信息检索的例子,对一次信息检索的请求(query),系统会预测出每个文档与当前检索关键词的相关程度,可以得到一个相关程度由高到低的排序。
MAP的计算过程:

第一次请求有五个相关的文档,相关的文档用阴影表示,得到排序1(Ranking #1),如果阈值设置使得排序中的第一个被预测为相关,其余为不相关,此时Recall为1/5,总共5个相关检测出了1个,Precision为1/1,预测的都是真实相关的。
如果阈值设置使得排序中的前两个被预测为相关,其余为不相关,此时Recall仍为1/5,Precision为1/2,预测的两个中有一个是相关的。以此类推可以计算得到设置不同的阈值下一个排序的的Recall值和Precision值。
在这个排序中,出现相关文本的位置的Precision的平均数是一次请求得到的当前排序的Average Precision,第一次请求的排序的AP1为5个相关文本所在位置的Precision相加除以5,第二次请求的排序的AP2为三个相关文本所在位置的Precision相加除以三。
对许多次请求的Average Precision的平均就是Mean Average Precision。
多分类任务的类比:
多分类任务的标签不止一个,系统会预测出测试样本在每个分类类别上的得分(confidence score),对多分类中的每一个类别,可以对测试样本的得分进行排序。
举个例子,多分类任务,假设共有20个测试样本,对于其中一个类别,每个样本的id,得分和标签如下(1代表是此类,0代表不是):
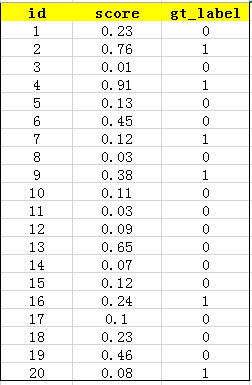
对得分进行排序如下:

插一句,最理想的排序结果是:1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0
对此类别AP的计算:

可见,在位置1,2,6,7,11,16上出现了标签是1的样本(类比于信息检索中的相关文档),将这些位置处的Precision求平均可以得到此类别的AP,为0.6621。
AP衡量的是系统在单个类别上的好坏,MAP衡量的是学出的模型在所有类别上的好坏,得到各个类别上的AP后,MAP就是取所有AP的平均值。
回归任务:
回归任务的评价指标关注预测值和真实值之间的差别,下面是三种衡量这之间差距的方法:
(r)MSE
(root) mean square error 是回归任务中最常用的指标,是预测值和真实值之差的平方的均值,再开根号就是rMSE。

这个指标比较好理解,而且可微,但对离群值(outliers)很敏感,对均值(mean)和标度(scale)都很敏感。
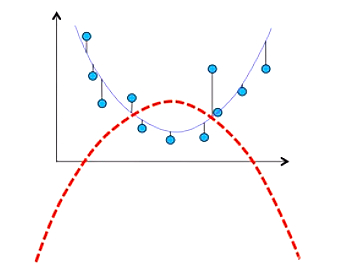
在MSE的计算中,一个离真实值很远的错误值会和许多许多小错误效果相同。预测书的价格的系统,A将其中99个都预测完全正确,只有一个差了10块,B预测的100本书都和真实价格差了1块,这两个系统的MSE是一样的值,因为MSE会取平方,所以对离群值会很敏感。下图展示了引入一个离群值(红色点)给以MSE为评价指标的系统的影响:加上红色点后,红色曲线的MSE将是最小的,比蓝色要小,系统会倾向于选择红色曲线。
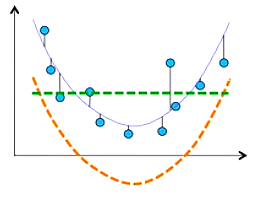
MSE对均值和标度也都很敏感。如下图,绿色的线是样本均值,黄色的虚线可以预测样本的趋势,但是黄色虚线的MSE比绿色虚线的MSE要高。对偏离样本均值的系统,不管系统能不能表达样本的规律,MSE都会很高。
因此也有人使用Relative squared error:

MAE
对预测值和真实值之差的绝对值求均值即为Mean Absolute Error。
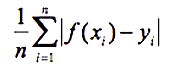
MAE对离群值没有MSE那么敏感了,但是同样对均值和标度很敏感,而且不能求导。但是对于优化器来说,优化目标可导是很重要的,这也是MSE被经常使用的原因。
对预测值和真实值之差的绝对值不求均值,而取中位数的话,即为Median Absolute Deviation(MAD):

MAD比MAE更加鲁棒,对离群值完全不敏感了,但依旧对均值和标度敏感,也同样无法求导,这使得MAD和MAE不被经常使用。
PCC/CC
相关系数(Correlation Coefficient),又称皮尔逊相关系数(Person's Correlation Coefficient,PCC),用r表示,定义如下:
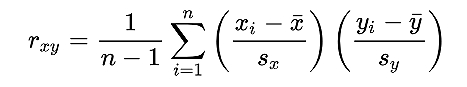
其中,
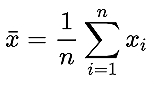
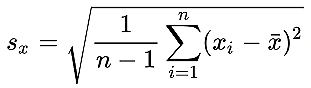
分别为均值和标准差。
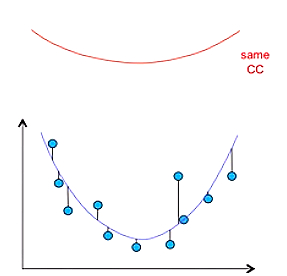
这个指标对均值和标度不敏感了,下图中的蓝线和红线的CC将会是一样的:
再多说一点相关系数(correlation coefficient)和协方差(covariance):
协方差定义如下:
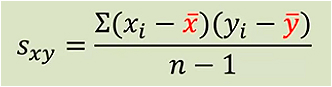
相关系数和协方差关系:
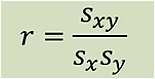
协方差是描述两个变量之间线性关系的量,协方差的英文covariance是由co(一起)和vary(变化)构成的,是在描述两个变量是如何共同变化的。
协方差的正负可以表示一个变量随另一个变量变化的方向(正、负、趋近于0),而不表示这种相关性的强度,而相关系数则不光可以表示方向,还可以表示强度。这是由于协方差的取值没有一个上限或者下限,其大小取决于变量的大小;而相关系数取值被归一化到了-1到1之间,与变量取值大小无关。
需要注意的是,相关系数可以表示变量相关性的强弱,但是不意味着相关系数的值的固定不变的统计学意义,相关系数的大小还和样本数量有关。根据经验,如果满足:
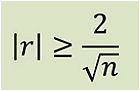
那么就认为相关性是存在的,其中,n为样本数量。
以上就是机器学习中分类任务和回归任务中常用的评价指标的总结。由于本人才疏学浅,精力有限,如果有什么不对的地方,感谢各位指出。
上面部分图片和例子来自Victor的视频教程:https://youtu.be/qFL2FEz9hxg,还参考了网上一些其他的资料。
(完)
